728x90
목차.
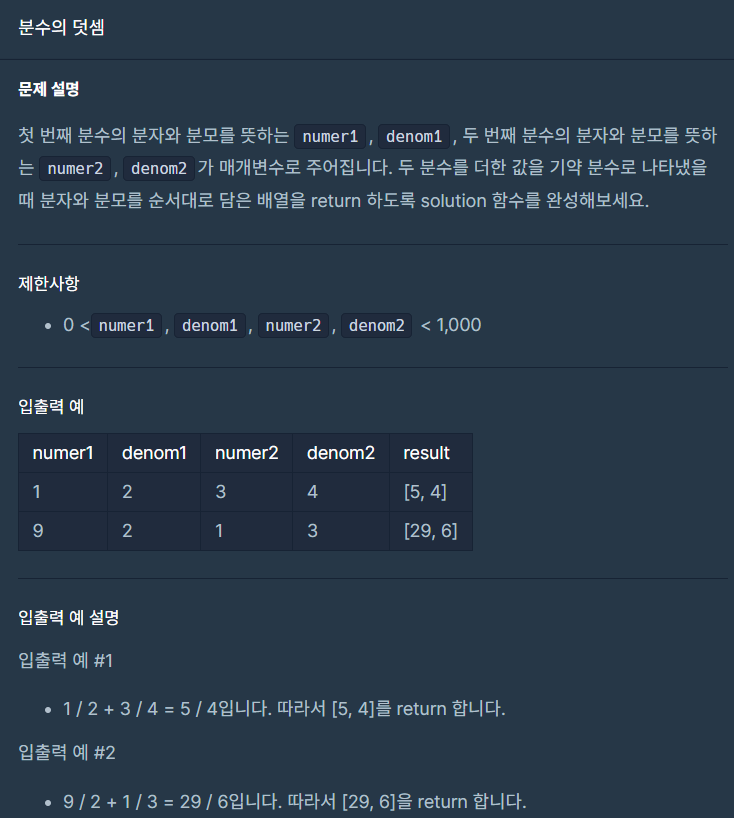
문제
풀이
분수의 덧셈을 구하기 위해서 최대 공약수를(GCD)를 구해야 합니다.
최대 공약수를 구하기 위해 반복문을 사용할 수 있지만,
시간 초과가 될 것입니다.
이럴 때 유클리드 호제법을 사용하면 빠르게 최대 공약수를 찾을 수 있습니다.
#include <string>
#include <vector>
using namespace std;
int gcd(int a, int b) { //유클리드 호제법
if (b == 0) return a;//b가 0이면 a가 최대 공약수
return gcd(b, a % b); //a와 b를 나눈 나머지로 재귀 호출
}
vector<int> solution(int numer1, int denom1, int numer2, int denom2) {
vector<int> answer;
int numer = numer1 * denom2 + numer2 * denom1;
int denom = denom1 * denom2;
int gcd_value = gcd(numer, denom); // 최대 공약수 구함
answer.push_back(numer / gcd_value);
answer.push_back(denom / gcd_value);
return answer;
}
분수를 더하기 위해서 각 분수의 분자와 분모를 공통분모로 맞추어야 합니다.
int numer = numer1 * denom2 + numer2 * denom1;
int denom = denom1 * denom2;
위 코드에서 각 분수를 공통 분모로 맞추고 더한 결과를 계산할 수 있습니다.
분수를 계산한 후, 최대 공약수(GCD)를 구해야 합니다.
최대 공약수는 분수를 기약분수로 만들기 위해 사용됩니다.
C++에서 유클리드 호제법을 사용하여 GCD를 구할 수 있습니다.
int gcd(int a, int b) { //유클리드 호제법
if (b == 0) return a;//b가 0이면 a가 최대 공약수
return gcd(b, a % b); //a와 b를 나눈 나머지로 재귀 호출
}
위 코드는 재귀 함수를 사용하여 GCD를 계산합니다.
'a'와 'b'는 GCD를 구하려는 두 정수입니다.
int gcd_value = gcd(numer, denom); // 최대 공약수 구함
answer.push_back(numer / gcd_value);
answer.push_back(denom / gcd_value);
위 코드에서 먼저 분자와 분모의 GCD를 구하고, 그 값을 사용하여 기약분수로 만든 후 결과를 반환합니다.
728x90
'코딩테스트' 카테고리의 다른 글
| [C++][Stack] 백준 10828번 : 스택(Stack) (0) | 2023.09.27 |
|---|---|
| C++ : 최빈값 구하기 (0) | 2023.09.15 |
| [백준][C++] 10798 문제 : 세로읽기 (0) | 2023.08.24 |
| [백준][C++] 4673 문제 : 셀프 넘버 (0) | 2023.08.24 |
| [C++][백준] 2839 문제 : 설탕 배달 (0) | 2023.08.15 |